Similar Triangles

Two triangles are Similar if the only difference is size (and possibly the need to turn or flip one around).

These triangles are all similar:

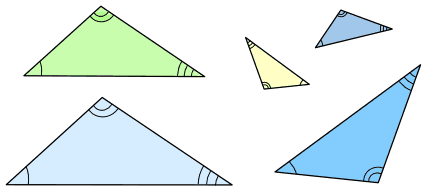
(Equal angles have been marked with the same number of arcs)

Some of them have different sizes and some of them have been turned or flipped.

Similar triangles have:

Corresponding Sides

In similar triangles, the sides facing the equal angles are always in the same ratio.

For example:

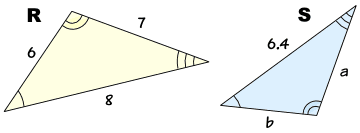
Triangles R and S are similar. The equal angles are marked with the same numbers of arcs.

What are the corresponding lengths?

The lengths 7 and a are corresponding (they face the angle marked with one arc)
The lengths 8 and 6.4 are corresponding (they face the angle marked with two arcs)
The lengths 6 and b are corresponding (they face the angle marked with three arcs)

It may be possible to calculate lengths we don't know yet. We need to:

Step 1: Find the ratio of corresponding sides in pairs of similar triangles.
Step 2: Use that ratio to find the unknown lengths.

We know all the sides in Triangle R, and
We know the side 6.4 in Triangle S

The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle R.

So we can match 6.4 with 8, and so the ratio of sides in triangle S to triangle R is:

6.4 to 8

Now we know that the lengths of sides in triangle S are all 6.4/8 times the lengths of sides in triangle R.

a faces the angle with one arc as does the side of length 7 in triangle R.

a = (6.4/8) × 7 = 5.6

b faces the angle with three arcs as does the side of length 6 in triangle R.

b = (6.4/8) × 6 = 4.8