How to Find the Mean
The mean is just the average of the numbers.
It is easy to calculate: add up all the numbers, then divide by how many numbers there are.
In other words it is the sum divided by the count.
Example 1: What is the Mean of these numbers?
6, 11, 7
- Add the numbers: 6 + 11 + 7 = 24
- Divide by how many numbers (there are 3 numbers): 24 / 3 = 8
The Mean is 8
Why Does This Work?
It is because 6, 11 and 7 added together is the same as 3 lots of 8:
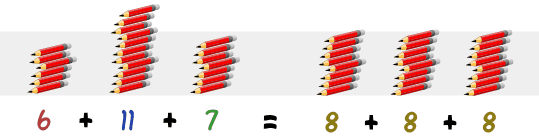
It is like you are "flattening out" the numbers
Example 2: Look at these numbers:
3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
The sum of these numbers is 330
There are fifteen numbers.
The mean is equal to 330 / 15 = 22
The mean of the above numbers is 22
Negative Numbers
How do you handle negative numbers? Adding a negative number is the same as subtracting the number (without the negative). For example 3 + (-2) = 3-2 = 1.
Knowing this, let us try an example:
Example 3: Find the mean of these numbers:
3, -7, 5, 13, -2
- The sum of these numbers is 3 - 7 + 5 + 13 - 2 = 12
- There are 5 numbers.
- The mean is equal to 12 ÷ 5 = 2.4
The mean of the above numbers is 2.4
The Mean from a Frequency Table
It is easy to calculate the Mean:
Add up all the numbers, then divide by how many numbers there are.
Example 1: What is the Mean of these numbers?
6, 11, 7
- Add the numbers: 6 + 11 + 7 = 24
- Divide by how many numbers (there are 3 numbers): 24 ÷ 3 = 8
The Mean is 8
But sometimes you won't have a simple list of numbers, you might have a frequency table like this (the "frequency" says how often they occur):
| Score | Frequency |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 4 |
| 4 | 2 |
| 5 | 1 |
(it says that score 1 occurred 2 times, score 2 occurred 5 times, etc)
You could list all the numbers like this:
| Mean = | 1+1 + 2+2+2+2+2 + 3+3+3+3 + 4+4 + 5 |
| (how many numbers) |
But rather than do lots of adds (like 3+3+3+3) it is often easier to use multiplication:
| Mean = | 2×1 + 5×2 + 4×3 + 2×4 + 1×5 |
| (how many numbers) |
And rather than count how many numbers there are, we can add up the frequencies:
| Mean = | 2×1 + 5×2 + 4×3 + 2×4 + 1×5 |
| 2 + 5 + 4 + 2 + 1 |
So let's calculate:
| Mean = | 2 + 10 + 12 + 8 + 5 | = | 37 | = 2.64... |
| 14 | 14 |
And that is how to calculate the mean from a frequency table!
Here is another example:
Example: Parking Spaces per House in Hampton Street
Isabella went up and down the street to find out how many parking spaces each house had. Here are her results:
| Parking Spaces | Frequency |
|---|---|
| 1 | 15 |
| 2 | 27 |
| 3 | 8 |
| 4 | 5 |
What is the mean number of Parking Spaces?
Answer:
| Mean = | 15×1 + 27×2 + 8×3 + 5×4 | = | 15+54+24+20 | = 2.05... |
| 15+27+8+5 | 55 |
The Mean is 2.05 (to 2 decimal places)
(much easier than adding all numbers separately!)
Notation
Now you know how to do it, let's do that last example again, but using formulas.
| This symbol (called Sigma) means "sum up" (read more at Sigma Notation) |
So we can say "add up all frequencies" this way:
(where f is frequency)
And we would use it like this:
Likewise we can add up "frequency times score" this way:
(where f is frequency and x is the matching score)
And the formula for calculating the mean from a frequency table is:
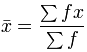
The x with the bar on top says "the mean of x"
So now we are ready to do our example above, but with correct notation.
Example: Calculate the Mean of this Frequency Table
| x | f |
|---|---|
| 1 | 15 |
| 2 | 27 |
| 3 | 8 |
| 4 | 5 |
And here it is:
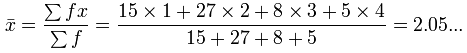
There you go! You can use sigma notation.
Calculate in the Table
It is often better to do the calculations in the table.
Example: (continued)
From the previous example, calculate f × x in the right-hand column and then do totals:
| x | f | fx |
|---|---|---|
| 1 | 15 | 15 |
| 2 | 27 | 54 |
| 3 | 8 | 24 |
| 4 | 5 | 20 |
| TOTALS: | 55 | 113 |
And the Mean is then easy:
Mean = 113 / 55 = 2.05...