Operations with Functions
 |
You can add, subtract, multiply and divide functions!
The result will be a new function.
|
Let us try doing those operations on f(x) and g(x):
Addition |
You can add two functions:
(f+g)(x) = f(x) + g(x)
Note: I put the f+g inside () so you know they both work on x.
Example: f(x) = 2x+3 and g(x) = x2
(f+g)(x) = (2x+3) + (x2) = x2+2x+3
Sometimes you may need to combine like terms:
Example: v(x) = 5x+1, w(x) = 3x-2
(v+w)(x) = (5x+1) + (3x-2) = 8x-1
The only other thing to worry about is the Domain (the set of numbers that go into the function), but I will talk about that later!
Subtraction |
You can also subtract two functions:
(f-g)(x) = f(x) - g(x)
Example: f(x) = 2x+3 and g(x) = x2
(f-g)(x) = (2x+3) - (x2)
Multiplication |
You can multiply two functions:
(f·g)(x) = f(x) · g(x)
Example: f(x) = 2x+3 and g(x) = x2
(f·g)(x) = (2x+3)(x2) = 2x3 + 3x2
Division |
And you can divide two functions:
(f/g)(x) = f(x) / g(x)
Example: f(x) = 2x+3 and g(x) = x2
(f/g)(x) = (2x+3)/x2
| (g º f)(x) |
Domain
It has been very easy so far, but now you must consider the DOMAINS of the functions.
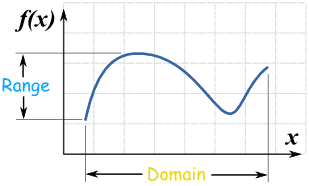 |
The domain is the set of all the values that go into a function.
The function must work for all values you give it, so it is up to you to make sure you get the domain correct!
|
Example: the domain for √x (the square root of x)
You cannot have the square root of a negative number (unless you use imaginary numbers, but we aren't doing that here), so we must exclude negative numbers:
The Domain of √x is all non-negative Real Numbers
On the Number Line it looks like:

Using set-builder notation it is written:
{ x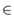
 | x ≥ 0}
| x ≥ 0}
Or using interval notation it is:
[0,+∞)
It is important to get the Domain right, or you will get bad results!
So how do you work out the new domain after doing an operation?
How to Work Out the New Domain
When you do operations on functions, you end up with the restrictions of both.
 |
It is like cooking for friends:
So what you cook can't have peanuts and also can't have dairy products.
|
Here is an example:
Example: f(x)=√x and g(x)=√(3-x)
The domain for f(x)=√x is from 0 onwards:

The domain for g(x)=√(3-x) is up to and including 3:
The new domain (after adding or whatever) is therefore from 0 to 3:
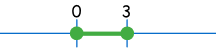
If you choose any other value, then one or the other part of the new function won't work.
In other words you want to find where the two domains intersect.
An Extra Rule for Division
There is an extra rule for division:
As well as restricting the domain as above, when we divide:
(f/g)(x) = f(x) / g(x)
we must also make sure that g(x) is not equal to zero .
Here is an example:
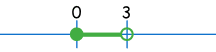
Example: f(x)=√x and g(x)=√(3-x)
(f/g)(x) = √x / √(3-x)
The domain for f(x)=√x is from 0 onwards:

The domain for g(x)=√(3-x) is up to and including 3:
But we also have the restriction that √(3-x) cannot be zero, so x cannot be 3:
(Notice the open circle at 3, which means not including 3)
So all together we end up with:
Summary
- To add, subtract, multiply or divide functions just do as the operation says.
- The domain of the new function will have the restrictions of both functions that made it.
- Divide has the extra rule that the function you are dividing by cannot be zero.