Fractions

A fraction is a part of a whole

Slice a pizza, and you will have fractions:

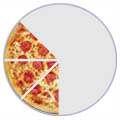1/2	1/4	3/8
(One-Half)	(One-Quarter)	(Three-Eighths)
The top number tells how many slices you have  The bottom number tells how many slices the pizza was cut into.

Equivalent Fractions

Some fractions may look different, but are really the same, for example:

4/8	=	2/4	=	1/2
(Four-Eighths)		Two-Quarters)		(One-Half)
	=		=

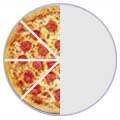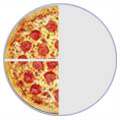It is usually best to show an answer using the simplest fraction ( 1/2 in this case ). That is called Simplifying, or Reducing the Fraction

Numerator / Denominator

We call the top number the Numerator, it is the number of parts you have.
We call the bottom number the Denominator, it is the number of parts the whole is divided into.

Numerator

Denominator

You just have to remember those names! (If you forget just think "Down"-ominator)

Adding Fractions

You can add fractions easily if the bottom number (the denominator) is the same:

1/4	+	1/4	=	2/4	=	1/2
(One-Quarter)		(One-Quarter)		(Two-Quarters)		(One-Half)
	+		=		=

Another example:

5/8	+	1/8	=	6/8	=	3/4
	+		=		=

Adding Fractions with Different Denominators

But what if the denominators (the bottom numbers) are not the same? As in this example:

3/8	+	1/4	=	?
	+		=

You must somehow make the denominators the same.

In this case it is easy, because we know that 1/4 is the same as 2/8 :

3/8	+	2/8	=	5/8
	+		=